Bamboo is coming
미적분학의 본질 | 3B1B, 4장 본문
제4장: 연쇄 법칙과 곱미분 법칙의 시각화
1. 함수의 결합 방식

합미분 법칙(sum rule), 곱미분 법칙(Product rule), 연쇄법칙
2. 합미분 법칙

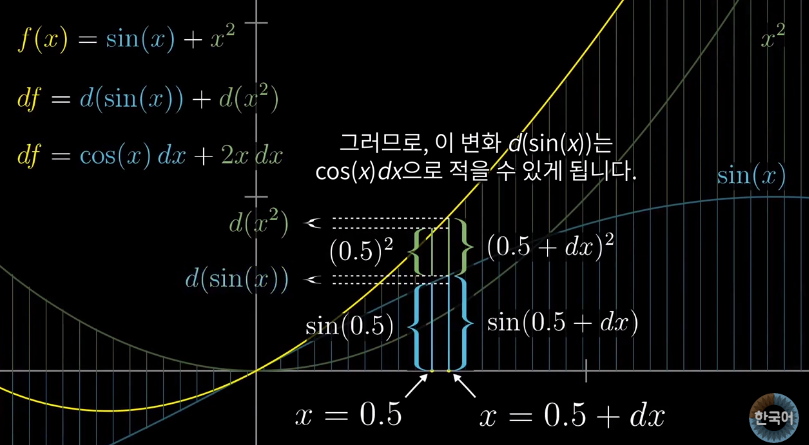

\(d(\sin(x))=df\):
- \(df = \frac{d}{dx}(\sin(x)) = \cos(x)\)
- 따라서, \(df = d(\sin(x)) = \cos(x)dx\)
* dx는 x의 변화 d(x)는 x의 변화에 따른 y의 변화 \(frac{df}{dx}\)는 도함수
* 도함수는 한점의 변화율에 근접한 상수값
결국 합미분 법칙은 함수 각자의 도함수의 합이 되는 것.
2. 곱미분 법칙
두 대상의 곱을 다룰 때 넓이를 구하는 문제로써 생각하는 것이 효과적. 따라서, 시각화는 넓이로 확인
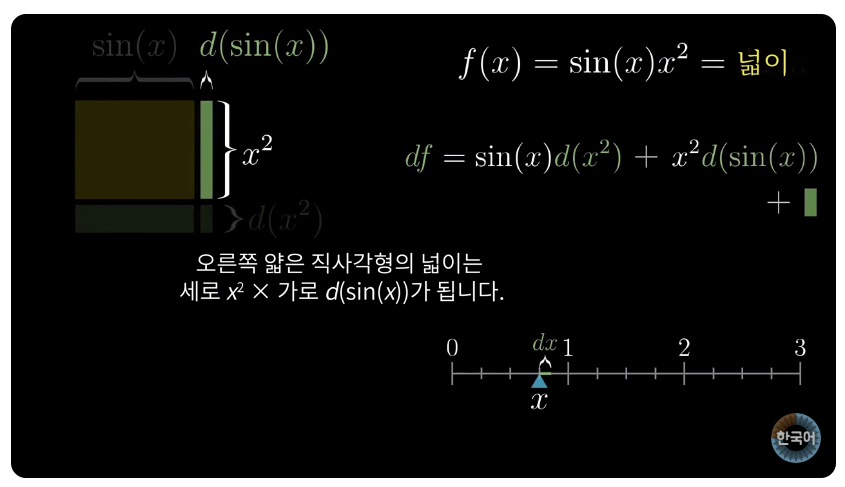
세로 변 y는 x에 종속적이므로 넓이로 표현 가능

x의 변화량을 dx라고 했을 때 변화한 크기는 오른쪽 직사각형 \(d(sin(x))\)에 기존 세로 높이\(x^2\)를 곱한 \(d(sin(x)x^2\)과, 아래쪽 직사각형 넓이 가로 \(sin(x)\) 세로 \(d(x^2) \)인 \(sin(x)d(x^2)\)을 각각 더해주면 미분 계산 기능
이를
\(d(\sin(x))\):
- \(\frac{d}{dx}(\sin(x)) = \cos(x)\)
- 따라서, \(d(\sin(x)) = \cos(x)dx\)

3. 합성함수(연쇄법칙)
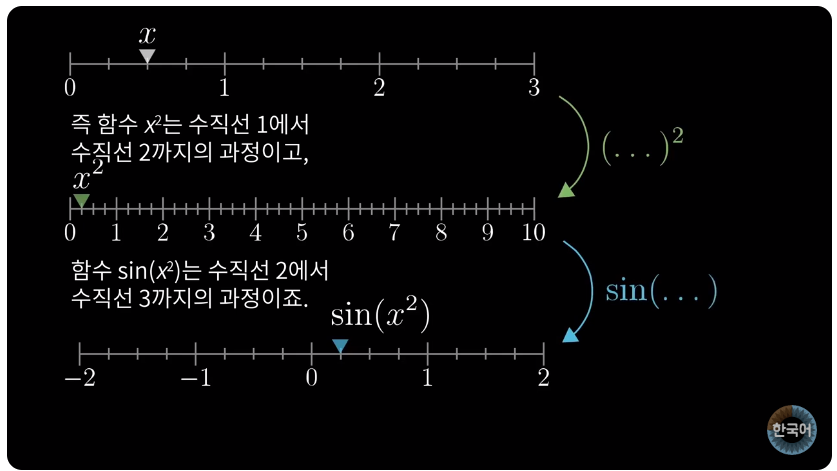

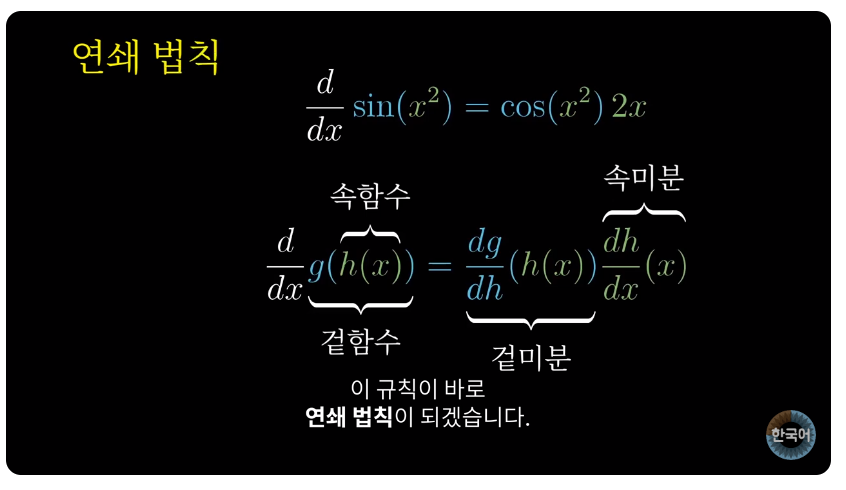
'수학' 카테고리의 다른 글
| 미적분학의 본질 | 3B1B, 6장 (0) | 2024.01.18 |
|---|---|
| 미적분학의 본질 | 3B1B, 5장 (0) | 2024.01.17 |
| 미적분학의 본질 | 3B1B, 3장 (0) | 2024.01.16 |
| 미적분학의 본질 | 3B1B, 2장 (0) | 2024.01.15 |
| 미적분학의 본질 | 3B1B, 1장 (0) | 2024.01.15 |
Comments




