Bamboo is coming
미적분학의 본질 | 3B1B, 3장 본문
미적분학의 본질 : 기하학을 통한 미분 공식, 3장
미분공식
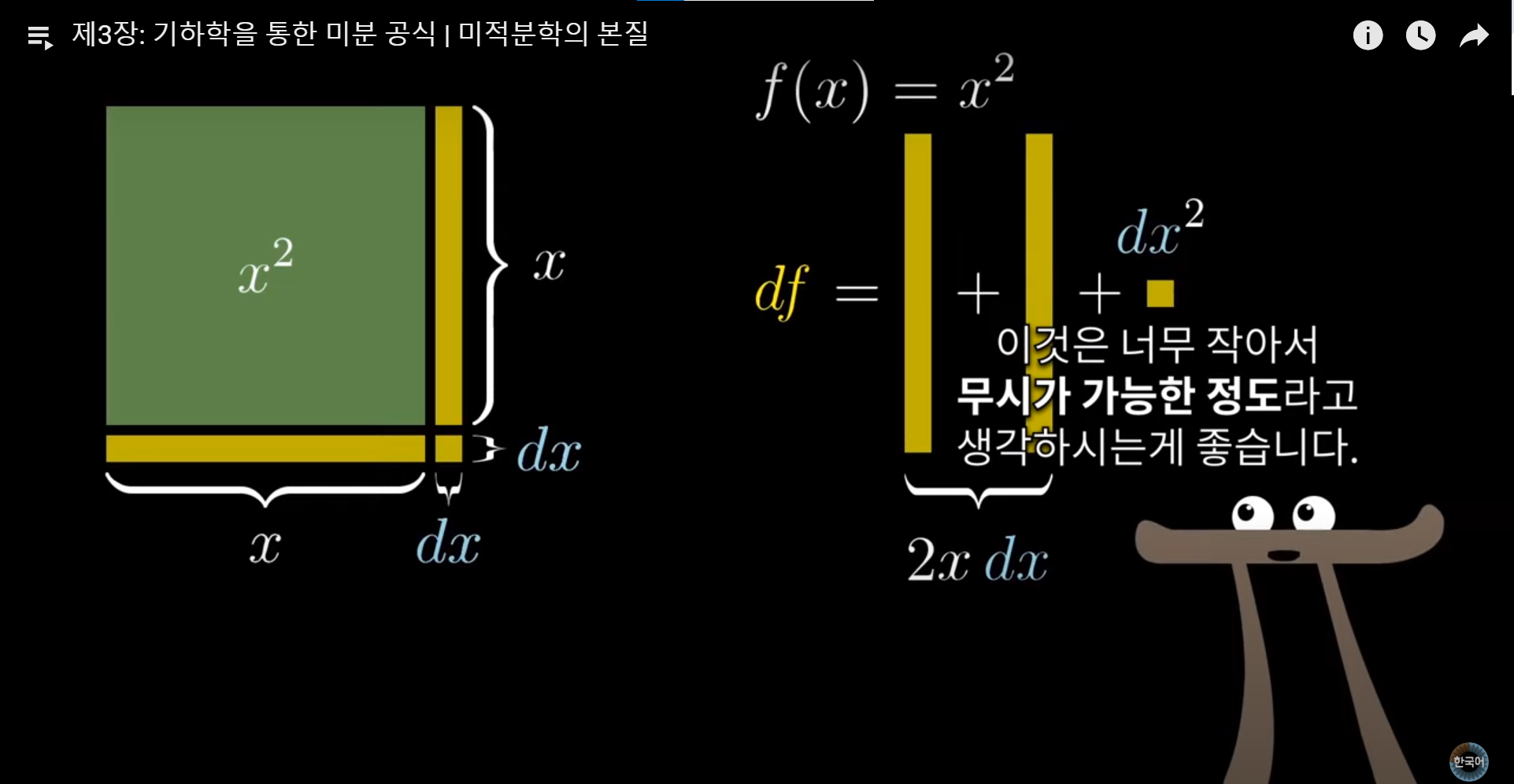
-> 2강 계산에서 나왔던 걸 참고하면 됨.

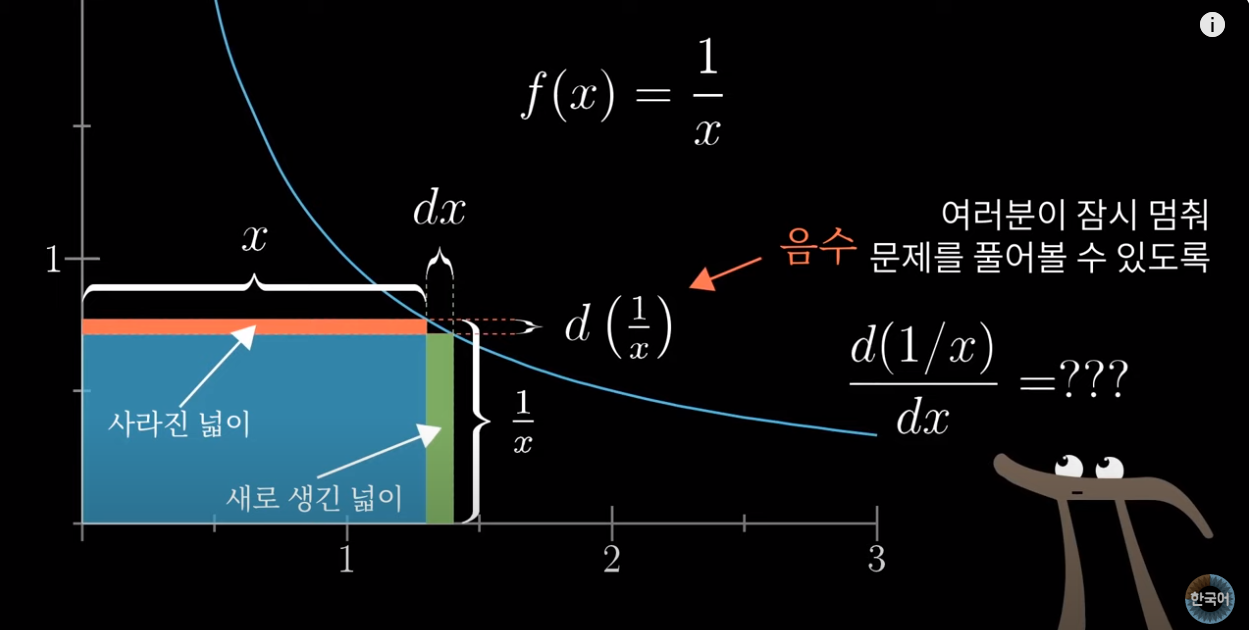
미분의 기본 정의에 따라, \( f(x) \)의 도함수 \( f'(x) \)는 다음과 같이 정의
\[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]
\( f(x) = \frac{1}{x} \)를 미분 정의에 대입
\[ f'(x) = \lim_{\Delta x \to 0} \frac{\frac{1}{x + \Delta x} - \frac{1}{x}}{\Delta x} \]
분수를 하나로 합치고 공통 분모를 찾기
\[ f'(x) = \lim_{\Delta x \to 0} \frac{\frac{x - (x + \Delta x)}{x(x + \Delta x)}}{\Delta x} \]
분자 간소화
\[ f'(x) = \lim_{\Delta x \to 0} \frac{\frac{-\Delta x}{x(x + \Delta x)}}{\Delta x} \]
분모에서 \(\Delta x\) 제거
\[ f'(x) = \lim_{\Delta x \to 0} \frac{-1}{x(x + \Delta x)} \]
극한 계산
\[ f'(x) = \lim_{\Delta x \to 0} \frac{-1}{x(x + \Delta x)} = \frac{-1}{x^2} \]
따라서, \( f(x) = \frac{1}{x} \)의 도함수 \( f'(x) \)는 \( \frac{-1}{x^2} =-x^{-2}\)
삼각함수의 도함수
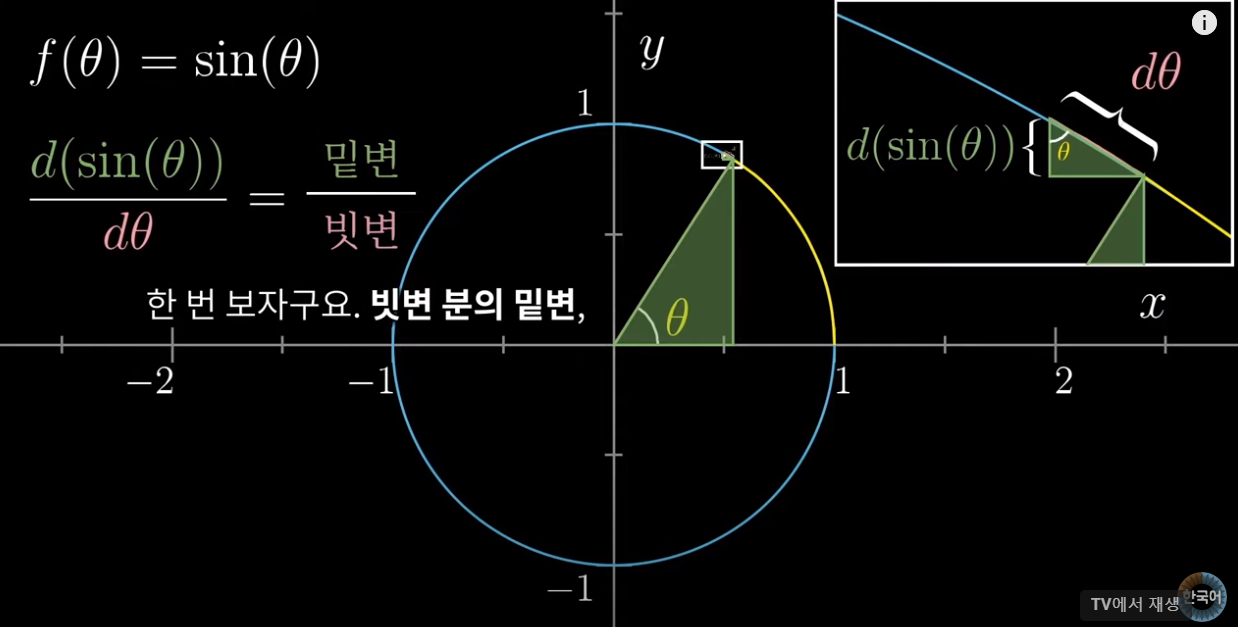
닮음비를 이용하여 구했을 때 빗변 분의 밑변이 cos의 식이 됨.
'수학' 카테고리의 다른 글
| 미적분학의 본질 | 3B1B, 5장 (0) | 2024.01.17 |
|---|---|
| 미적분학의 본질 | 3B1B, 4장 (0) | 2024.01.17 |
| 미적분학의 본질 | 3B1B, 2장 (0) | 2024.01.15 |
| 미적분학의 본질 | 3B1B, 1장 (0) | 2024.01.15 |
| 하버드 확률론 기초 STAT 110 - 3강 (0) | 2024.01.15 |




