Bamboo is coming
확률과 통계 본문
이산(떠날 이, 흩을 산; 떨어져 흩어짐)
──── INDEX ───
1. 경우의 수
1.1. 순열(permutation)
1.2. 조합(combination)
1.2.1. 다항계수(multinomial coefficient)
1.2.2. 이항계수(bionomial coefficient)
2. 확률(Probability)
2.1. 배경 용어
2.2. 확률변수(Random variable)
2.3. 확률분포(Probability Distribution)
2.3.1. 이산확률분포(Discrete Probability Distribution)
2.3.2. 이항분포(Binomial Distribution) B(n,p)
2.3.2. 확률질량함수(probability mass function, PMF)
2.4. 연속확률분포(continuous probability distribution)
2.4.1. 확률밀도함수(probability density function, PDF)
2.4.2. 정규 분포(normal distribution)
─── INDEX ───
1. 경우의 수
1.1. 순열(permutation)
def. 서로 다른 물건들 중 몇 가지 대상을 뽑아 일렬로 나열하는 것을 순열이라고 한다.
prof. n개의 서로 다른 원소를 가진 집합에서 r개의 서로 다른 대상들을 선택하여 배열하는 가능한 모든 경우들을 생각해 보자.
먼저, 첫 번째 원소는 n가지 방법으로 선택할 수 있다. 두 번째 원소는 첫 번째 선택된 원소와 달라야 하므로 (n-1)가지 방법으로 선택할 수 있다. 나머지 원소들을 선택하는 방법의 수도 같은 방식으로 결정되며, 마지막 r번째 원소는 (n-(r-1)))가지 방법으로 선택할 수 있다. 따라서 곱의 법칙에 의하여 r개를 선택하는 방법의 수는 \((n(n-1)(n-2)\ldots (n-r+1))\)가지가 된다.
note. 이때 서로 다른 n개의 물건들 중 k개를 뽑아 일렬로 나열하는 방법의 수를 기호 \( P(n,r) \text{또는 } _nP_r \text{또는}(n)_r\)로 나타낸다.
\[ P(n,r) = _nP_r = n(n-1)(n-2) \ldots (n-r+1) = \frac{n!}{(n-r)!} \]
ex. 원준이는 서로 다른 수학책 17권을 가지고 있다. 수학책 중 여섯 권을 골라 책장의 선반 위에 꼽는 방법의 수는 몇 가지일까?
서로 다른 17권의 책 중 여섯 권을 선택하여 배열하는 방법의 수이므로 \(P(17, 6)=17×16×15×14×13×12\)이다.
1.2. 조합(combination)
def. 서로 다른 원소를 가진 집합에서 원소들을 택하여 만든 부분집합을 조합(combination)이라고 한다.
proof. P(n,r)는 먼저 C(n,r)가지 방법으로 r개의 원소를 가진 부분집합을 고른 후, 선택된 r개의 원소들을 r!가지 방법으로 배열하여 구할 수 있다. 따라서 \(P(n,r) = C(n,r)r!\)이므로 \(C(n,r) = \frac{P(n,r)}{r!}=\frac{n!}{r!(n-r)!}\)이다.
특히, \(C(n,0)=1,C(n,1)=n, C(n,n)=1\)이다.
note. n개의 원소를 가진 유한집합에서의 r조합의 수를 \(C(n,r) \text{또는}_nC_k 또는 \begin{pmatrix} n \\ r \end{pmatrix}\)로 나타낸다.
\[C(n,r)=_nC_k=\frac{1}{k!}{_nP_k}=\frac{1}{k!}\frac{n!}{(n-k)!}=\frac{n!}{k!(n-k)!}\]
ex. 알파벳 a, b, c, d, e에서 서로 다른 두 개의 알파벳을 뽑는 방법의 수는 몇 가지일까? 서로 다른 다섯 개의 알파벳 중 두 개를 뽑는 방법의 수이므로 \(C(5,2)=_5C_2=\frac{5\times 4 \times 3 \times 2 \times 1}{(2 \times 1)(3 \times 2 \times 1)} = 10\)이다.
1.2.1. 다항계수(multinomial coefficient)
def. 다항계수란 음이 아닌 정수 n,k에 대해 이항계수는 \((x+y+z)^n\)와 같은 다항식을 전개했을 때 나타나는 각 항의 계수로 정의한다.
여기서 "다항"이란 여러 개의 항을 의미한다.
항이 각각 선택지로 분류되어 세 가지 이상의 선택지가 있는 상황 예를 들면 "n개의 서로 다른 항목을 r개의 그룹으로 나누는 방법의 수"를 나타낸다.

ex.

1.2.2. 이항계수(bionomial coefficient)
def. 이항계수란 음이 아닌 정수 n,k에 대해 이항계수는 \((1+t)^n\)을 전개했을 때 \(t^k\)의 계수로 정의한다.
여기서 "이항"이란 두 개의 항을 의미한다.
이항계수가 조합으로 해석되는 이유는 \((x + y)^n = x^n + \binom{n}{1}x^{n-1}y + \binom{n}{2}x^{n-2}y^2 + \cdots + y^n \) 으로 항들의 계수와 n개의 서로 다른 요소 중에서 k개를 순서에 관계없이 선택하는 방법의 수와 일치하기 때문이다.
이항 분포에서 사용되며, 주로 "n개 중에서 k개를 선택하는 방법의 수"로 해석된다
ex.
\((x + y)^2 = x^2 + 2xy + y^2\)
\(1 = \binom{2}{0}, \quad 2 = \binom{2}{1}, \quad 1 = \binom{2}{2}\)

2. 확률
기댓값, 평균
평균은 변수의 총합/변수의 수고,기댓값은 변수*변수의 확률을 모두 더해 변수의 수로 나눠준다.
이러한 의미에서 기댓값을 가중평균이라고 부른다.
2.1. 배경 용어
- Random Experiment(확률실험)
그 결과를 예측할 수 없는 실험 - Sample Space(표본공간)
확률실험에서 발생 가능한 모든 결과 $\Omega$ - Event(사건)
subset of sample space, 표본 공간의 부분 집합, 즉 관심을 갖는 실험의 결과 - Elementary Event(근원사건)
사건 가운데 하나의 원소로 이루어진 사건, 근원 사건 전체의 집합을 표본공간으로도 정의함
동전을 한 번 던져 윗면을 관찰하는 시행에서 앞면을 $H$, 뒷면을 $T$라고 하면, 전체사건은 $S={H,T}$이고
근원사건은 ${H}, {T}$이다.
2.2. 확률변수(Random variable)
def. 주어진 사건에 대한 특정 경우를 정의역(domain)으로 취하는 함수로 각각의 경우에 따라 확률 값을 가진다.
sample space를 정의역(domain)으로 하고 실수 전체 집합을 공역(codomain)으로 하는 함수다. 그러나 변수의 역할을 하므로 확률변수라고 불린다.
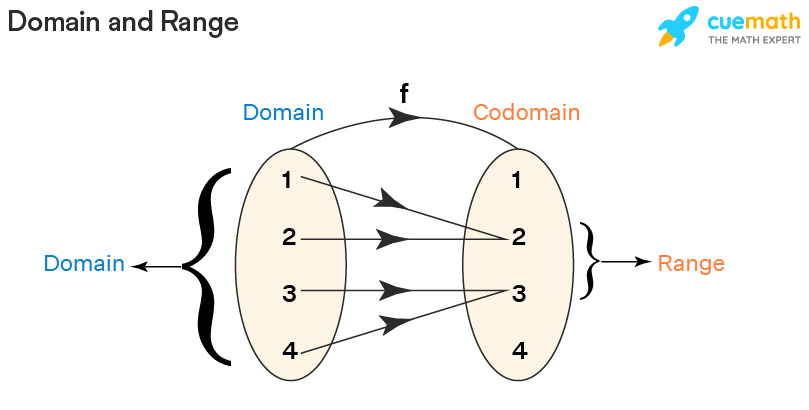
ex. 동전 두 개를 던져 앞면이 나오는 횟수를 확률변수 X라고 했을 때, 동전 두 개를 던지면 다음과 같이 네 가지의 경우가 발생한다.
sample space ={뒤-뒤, 앞-뒤, 뒤-앞, 앞-앞}
확률변수 X는 이들을 정의역으로 취하는 함수이다.
예를 들어 (뒤-뒤)를 취하면 모두 뒷면이 나오는 경우로 X(뒤-뒤)=0이 된다. 마찬가지로 X(앞-뒤)=1, X(뒤-앞)=1, X(앞-앞)=2임을 알 수 있다. 그러면 확률변수 X가 취할 수 있는 값은 X=0, X=1, X=2와 같이 모두 세 가지가 된다. 확률변수에서 (앞-뒤), (뒤-앞)과 같은 특정 사건 결과는 생략하고 X=x와 같이 취하는 값만 표기한다.
확률변수 = { 0, 1, 2 }
2.3. 확률분포(Probability Distribution)
def. 확률변수 X가 특정한 값을 가질 확률을 나타내는 분포.
확률분포란 간단하게 말해 확률변수 X의 함수라고 할 수 있다. 확률변수 X는 특정한 값을 가지게 되는데, 그 값을 가질 확률들은 일종의 함수와 같이 어떤 분포를 갖게 된다.
ex. 위의 예시와 같이 동전 두 개를 던져 앞면이 나오는 횟수를 확률변수 X라고 했을 때, 확률변수 X = { 0, 1, 2 }
- X(뒤-뒤) = 0일 확률, P(X=0) = (1/2)² = 1/4
동전의 앞, 뒷면 중에서 뒷면이 나올 확률은 1/2, 두 개의 동전 모두 뒷면이 나올 확률은 (1/2)² - X(앞-뒤) or X(뒤-앞) = 1일 확률, P(X=1) = 1/2
동전의 앞, 뒷면 중에서 앞면이 나올 확률은 1/2, 두 개의 동전 중 한개만 앞면이 나올 확률은 (1/2)¹ - X(앞-앞) = 2일 확률, P(X=2) = (1/2)² = 1/4
동전의 앞, 뒷면 중에서 앞면이 나올 확률은 1/2, 두 개의 동전 모두 앞면이 나올 확률은 (1/2)² - 확률분포 X에 대한 분포표
| X | 0 | 1 | 2 | 계 |
| P | 1/4 | 1/2 | 1/4 | 1 |
확률변수는 취하는 정의역의 성질에 따라 이산확률변수와 연속확률변수로 나뉜다.
만약 확률변수 X가 X={0, 1, 2, 3, ··}이나 X={2, 3, 4}등과 같이 셀 수 있는 값을 취할 때는 이산확률변수라 한다. 동전을 던지거나 주사위를 던지는 사건 등도 하나둘씩 셀 수 있는 경우이므로 이산확률변수에 해당한다. 또한 반드시 정수의 값이 아니어도 유한한 개수의 값을 취할 때는 이산확률변수가 된다.
반면 확률변수 X가 키, 몸무게, 시간과 같이 셀 수 없고 연속적인 값을 취할 때에는 이를 연속확률변수라 한다. 연속확률변수는 확률변수가 특정한 값을 취할 때의 확률이 아닌 특정 구간 내에서의 확률 값을 구하며, P(a≤X≤b)와 같이 표기한다. 예컨대 확률변수 X가 어떤 집단의 키를 나타낼 때 키가 160에서 165일 확률은 P(160≤X≤165)로 나타낸다.
2.3.1. 이산확률분포(Discrete Probability Distribution)
def. 확률변수가 이산집합이어서 유한집합이거나 가산일 때 이에 대응하는 확률분포를 이산확률분포라고 한다.
이산확률분포는 확률질량함수(probability mass function, PMF)를 통해 표현 가능하다.

ex.
\[ f_{X}(x)={\begin{cases}{\frac {1}{2}},&x\in \{0,1\},\\0,&x\notin \{0,1\}.\end{cases}} \]
이산확률분포의 기댓값: \( E(X) = \sum X. P(X) \)
이산확률분포의 분산: \( V(X) = E(X^2)-(E(X))^2 \)
이산확률분포의 표준편차: \( \sigma (X) = \sqrt{V(X)} \)
분산의 성질
①. \(E(aX+b)=aE(x)+b \)
상수는 앞으로 나오고 상수의 기댓값은 상수이다.
②. \( V(aX+b)=a^2V(X) \)
상수를 제거하고 전개하면 해당 식이 나온다.
③. \( \sigma \left(aX+b\right)=\left|{\sigma }\right|V\left(X\right) \)
②에 루트를 씌우면 \( \sigma^2이 \left|{\sigma }\right \)이 되고, 분산에 루트를 씌우면 표준편차가 된다.
2.3.2. 이항분포(Binomial Distribution) B(n,p)
이산확률분포의 일종은 이항분포
어떤 일을 1번 시행할 때 일어날 확률(되는 확률) p . 안되는 확률 q를 n번 시행했을 때 일어난(된) 확률변수를 X라 한다.
(매 시행마다 일어날 확률은 반드시 일정해야한다)
성공확률이 M인 베르누이 시행을 N번 반복하는 경우 N번 성공한 횟수를 확률변수 X라고 한다면 X의 값은 0~N까지의 정수 중에 하나
이런 확률 변수를 이항분포를 따르는 확률변수라고 함.
$X~B(X;N,M)$
조건
1. n번의 독립시행
2. 관심사건 A일 때, \( P(A) = p, P(A^c)=1-p \) (A가 일어났거나, 일어나지 않았거나)
3. n번 중 A가 일어난 횟수 = 확률변수(random variable)
확률변수가 X일때, 확률질량함수와 독립시행확률과 동일함
P(X=K)
Def.
B(n,P)
\[ P(X=r) = _nC_r*p^2q^{n-r} \]
ex. 동전을 2개 던지는 것을 5번 시행했을 때 둘다 앞면이 나오는 횟수를 확률변수 X라 할 때
P = 1/4, q= 3/4, n=5, X={0,1,2,3,4,5}, B(5,1/4)
일어날 확률이 2번일 확률
\[ P(X=2) = _5C_2*(\frac{1}{2})^2(\frac{3}{4})^3\]
평균 E(x) = np
분산 v(x) = npq
표준분산 \root{npq}
2.3.2. 확률질량함수(probability mass function, PMF)
Def.
확률 변수 \(X:S\to {\mathbb {R}} \)가 표본 공간 (sample space) 에 의해 정의되는 이산 확률 변수일 때, 확률 질량 함수 \( f_{X}(x):{\mathbb {R}}\to [0,1]$는 $f_{X}(x)=\Pr(X=x)=\Pr(\{s\in S:X(s)=x\}) \)이다.

2.4. 연속확률분포(continuous probability distribution)
그 중에 확률변수가 가질 수 있는 값이 uncountable할 때 연속확률분포라고 한다.
ex) 시간, 몸무게, 키
연속확률분포의 확률은 구간의 넓이로 구한다.
이산확률분포의 일종은 이항분포이고, 연속확률분포의 일종은 정규분포
2.4.1. 확률밀도함수(probability density function, PDF)
데이터의 분포를 표로 나타낼 수 없어 그래프 즉 함수로 나타낸다.
연속확률분포의 표현은 확률밀도함수로 할 수 있다.
확률밀도함수의 성질
①. $f(x) \geq 0$, 확률은 음수일 수 없다.
②. $P(a \leq X \leq b) = a \leq x \leq b$ 에서 곡선과 X축 사이의 넓이
③. 시작~끝의 확률은 반드시 1 = 전체 넓이는 1
④. $P(X=a)=0$, 어떤 점에서의 확률은 0이 된다.
ex) 버스를 기다리는 시간을 X로 두면 딱 정확하게 10분이 걸릴 확률은 한없이 작음
따라서 \( P(a \leq X \leq b) = P(a < X \leq b) = P(a \leq X < b) = P(a < X < b) \)
왜? 점이 포함되나 포함되지 않나 확률에는 변동이 없다.

ex.
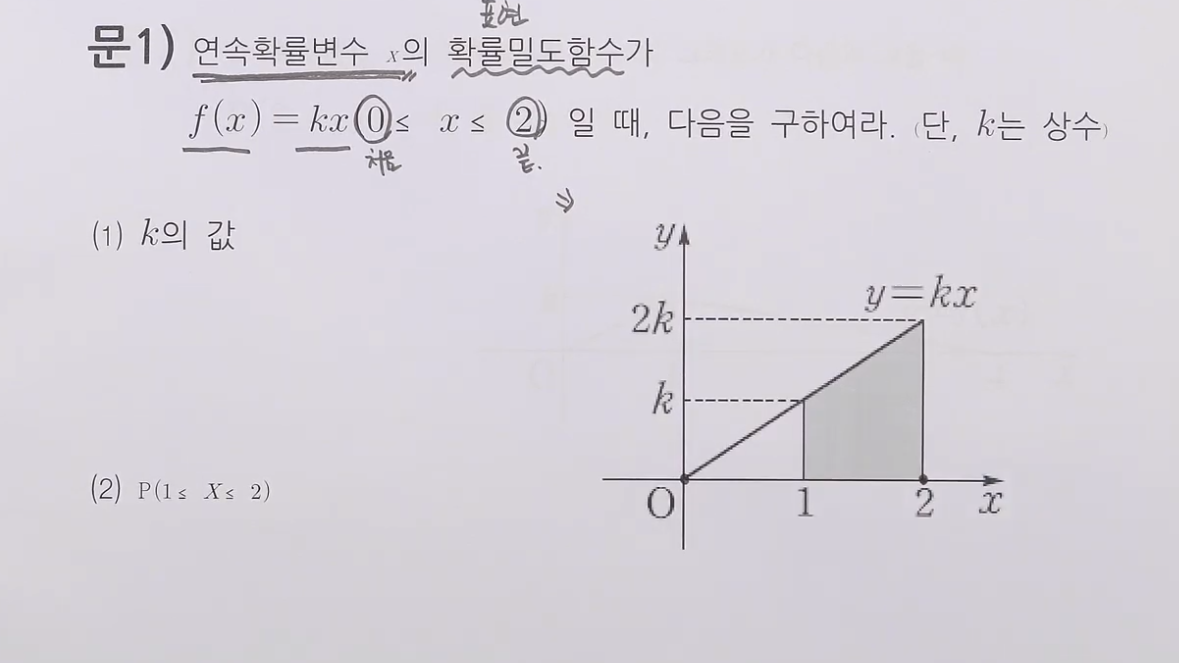
2.4.2. 정규 분포(normal distribution)
또는 가우스 분포(Gaussian distribution)는 연속 확률 분포의 하나이다.
정규분포는 확률밀도함수의 일종인데 종 모양의 모양을 가진 그래프를 의미한다.
정규분포는 2개의 매개 변수 평균 $\mu$ 과 표준편차 $\sigma$에 대해 모양이 결정되고, 이때의 분포를 ${\mathrm {N}}(\mu ,\sigma ^{2})$로 표기한다. 특히, 평균이 0이고 표준편차가 1인 정규분포 ${\mathrm {N}}(0,1)$을 표준 정규 분포(standard normal distribution)라고 한다.

정규분포는 절대근사한다.
정규분포는 평균과 표준편차가 주어져 있을 때 엔트로피를 최대화하는 분포이다.
정규분포곡선은 좌우 대칭이며 하나의 꼭지를 가진다.
정규분포는 중앙치에 사례 수가 모여있고, 양극단으로 갈수록 X축에 무한히 접근하지만 X축에 닿지는 않는다.
Note.
\[ N(평균, 표준편차^2) = N(m,\sigma^2) \]
정규분포의 평균은 그래프의 가장 높은 지점
m+\sigma
대칭임.
정규분포의 구간은 모두 동일한 넓이를 가짐.
N(0,1^2) 표준 전규분포
표준정규분포표를 따르도록 계산
N(20,4^2)
이 때, 변수 x가
표준화공식
\frac{x-m|{\sigma}
정규분포를 표준정규분포로 옮길수 있음
임의추출(표본을 뽑는다)
변수가 x바로 바뀜(표본평균)
E(x바)=평균은 그대로
분산은 n으로 나눈다
표준편차는 루트n으로 나눈다.
통계적 추정/모평균의 추정
n명 임의 추출~ 평균
모평균 m,
n명의 임의추출 표본평균 x바
신뢰구간
https://hsm-edu-math.tistory.com/592
다항계수_네이버지식백과(수학백과)
조합_네이버 지식백과(수학백과)
이항계수의 성질_유튜브(수악중독)
근원사건_네이버 지식백과
https://datalabbit.tistory.com/17
'수학' 카테고리의 다른 글
| 신호처리 (0) | 2023.09.05 |
|---|---|
| MCMC(Markov Chain Monte Carlo) (0) | 2023.09.05 |
| 선형 회귀, 로지스틱 회귀 (0) | 2023.08.21 |
| 확률, logit 로짓, (0) | 2023.08.17 |
| 인공지능을 위한 기초수학 입문(함수, 벡터, 행렬) (0) | 2023.08.16 |
