Bamboo is coming
인공지능을 위한 기초수학 입문(함수, 벡터, 행렬) 본문
x의 값들의 집합을 f의 정의역(domain), y의 값들의 집합을 f의 치역(range)
다항함수(polynomial function)
- 다항식으로부터 유도되는 함수
- \[f(x)=mx+b\]
- \[f(x)=ax^2+bx+c\]
유리함수(rational functions)
- 두 다항함수의 비(ratio)로 표현되는 함수
- \[y=f(x)=1/x\]
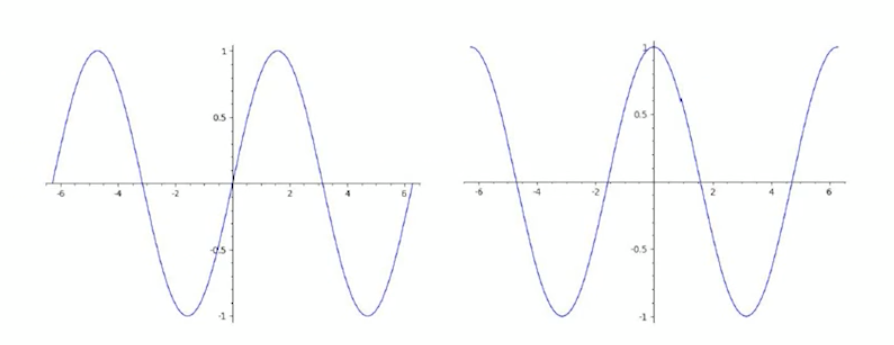
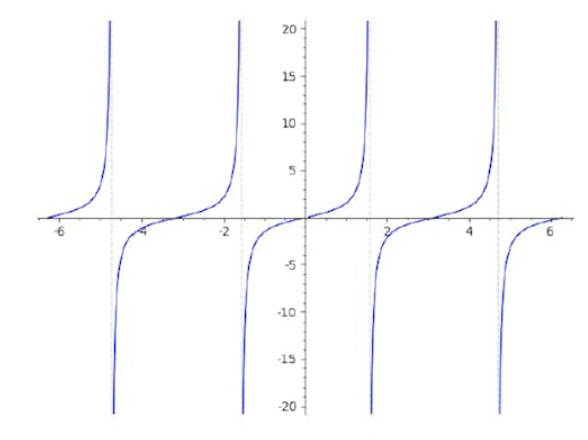
삼각함수(trigonometric functions)
- 삼각함수는 각의 크기에 따라 변화하는 삼각비를 나타내는 함수로 일정한 패턴이 반복되는 주기함수이다.
- \(sinx\)와 \(cosx\)의 주기는 \(2pie\)이고 y가 -1부터 1까지의 값을 취할 수 있다.
- \(tanx\)의 주기는 \(pie\)이고, y로 모든 실수 값을 취할 수 있다.(무한대)
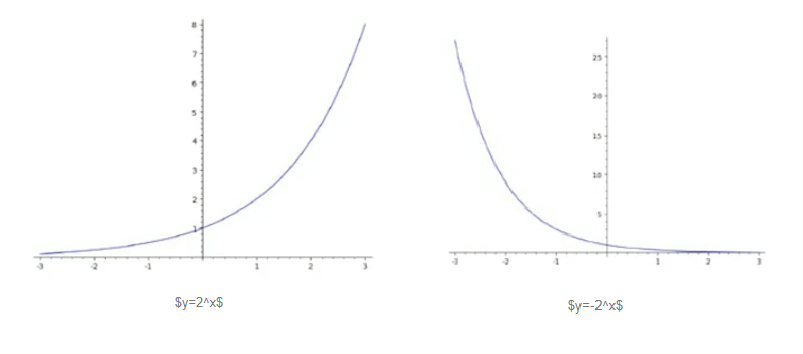
지수함수(exponential fucntion)와 로그함수(logarithm)
- \[y=f(x)=a^x\]
- 지수함수는 a>1일 때 증가함수, 0<a<1일 때 감소함수
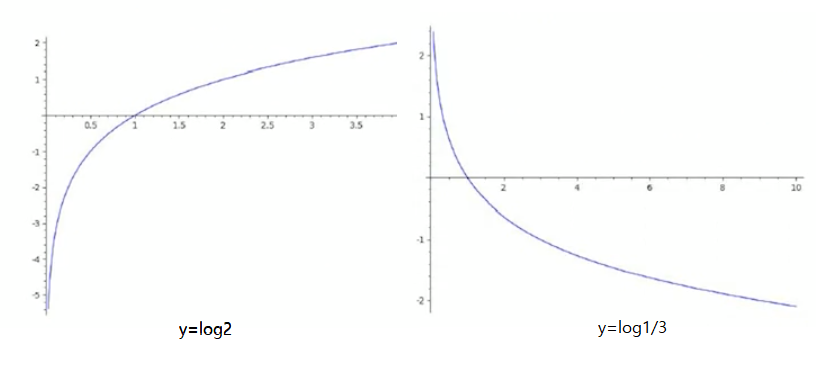
- \[y=f(x)=log_{a}x\]
- 로그함수는 밑(base)가 a이고 진수(exponent)가 x인 함수
- 로그함수는 지수함수의 역함수로 a>1일때 증가함수, 0<a<1일때 감소함수
벡터
- \(a_1,a_2\)를 성분으로 하는 데이터 \((a_1,a_2)\)는 좌표평면 상의 한 점 A를 나타낸다. 이때 시작점을 원점 O, 끝점을 A로 하는 화살표로 나타낸 것을 벡터(vector)라고 하고 \(vec{OA} =a=(a_1,a_2)\)로 표기한다.
그리고 벡터를 이루는 각각의 성분은 하나의 숫자로 이루어져 있는데 이를 스칼라(scalar)라고 한다. - 직사각형은 행렬(matrix), 행벡터는 1Xn 행렬, 열벡터는 nX1 행렬으로 볼 수 있음
- 3차원의 행렬은 3-D 텐서(tensor)
- 1-D tensor = vector, 2-D tensor = matrix
벡터의 연산
- 실수배(scalar multiple) 실수 k와 벡터(a,b)의 곱
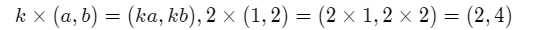
- 덧셈 : 두 벡터 (a,b), (c,d)에 덧셈
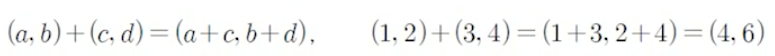
행렬의 연산
- 실수배(scalar multiple) 실수 k와 벡터(a,b)의 곱
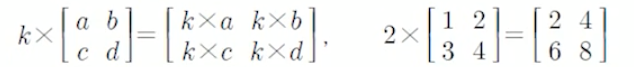
- 덧셈 : 두 벡터 (a,b), (c,d)에 덧셈

- 곱셈(product)

전치행렬(transpose matrix)
- 행렬 A의 행과 열을 바꾸어 얻어진 행렬을 \(A^T\)로 나타낸다.
- 대각선 성분은 변하지 않고 (i,j) -> (j,i)

대각선 행렬(diagonal matrix)
- 주대각선성분 이외의 모든 성분이 0인 정사각행렬,
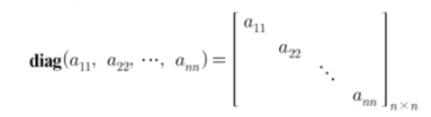
단위행렬(identity matrix)
- 주대각선성분이 모두 1인 대각선 행렬 \(I_n\)
- 단위행렬은 어떤 행렬을 곱해도 같은 행렬이 나온다.
- 항등원은 연산에서 시작점 또는 기준이 되는 요소로 덧셈에서 항등원은 0, 곱셉에서 항등원은 1이다. 이 값들은 숫자와 조합해도 그 숫자를 변화시키지 않는다.
- 항등원을 사용하면 연산의 역원도 정의할 수 있다. (역원: 어떤 연산 결과를 되돌릴 수 있는 값)
- \[I_n = \begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix} \]

삼각행렬
- 하삼각행렬(lower triangular matrix):: 주대각선 위의 모든 성분이 0인 정사각행렬
- 상삼각행렬(upper triangular matrix): 주대각선 아래의 모든 성분이 0인 정사각행렬

대칭행렬(symmetirc matrix)
- \(A^T=A\)을 만족하는 정사각행렬
- 모든 \(a_ij = a_ji\) 성립
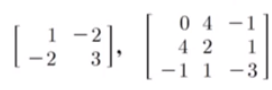
역행렬(inverse matirx)
- \(n \times n\) 정사각행렬 A에 대하여 다음을 만족하는 행렬 B가 존재하면 A는 가역(invertible, nonsingular)이라고 한다.
- A와 곱해서 단위행렬이 되는 B가 존재하면 A는 가역이다.

이때 B를 A의 역행렬이라 하며, \(A^-1\)로 나타낸다. 이러한 B가 존재하지 않으면 A는 비가역(noninvertible) 또는 특이행렬(singluar matrix)이라고 한다.

참고
http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_45+2023_T1/course/
강좌 | SKKU_45 | K-MOOC
www.kmooc.kr
'수학' 카테고리의 다른 글
| 선형 회귀, 로지스틱 회귀 (0) | 2023.08.21 |
|---|---|
| 확률, logit 로짓, (0) | 2023.08.17 |
| Bayesian Neural Network (0) | 2023.08.16 |
| 이산확률분포 (0) | 2023.07.26 |
| 베이즈 정리 (0) | 2023.07.13 |
Comments
